WhakamĀrama Āpitihanga
Ko te whakaatu i ngā whārite tukutahi ki te kauwhata tētahi ara whakaoti. Hei tauira:
x | –3 | –2 | –1 | 0 | 1 | |
whārite 1 (kākāriki) | y = x + 2 | –1 | –0 | 1 | 2 | 3 |
wharite 2 (whero) | y = –2x – 1 | 5 | 3 | 1 | –1 | –3 |
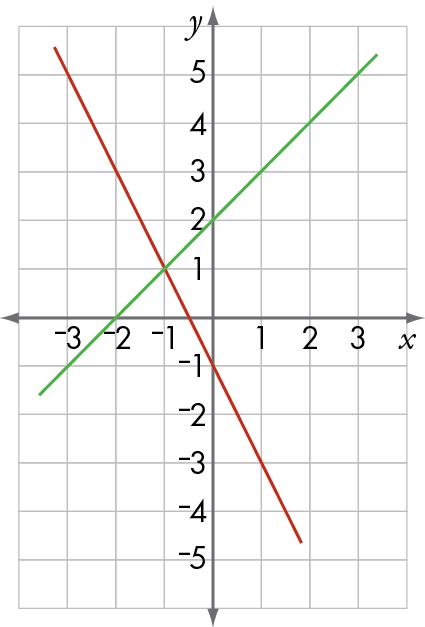
Ko te wāhi e pūtahi ana ngā rārangi e rua, koia te otinga tukutahi o ngā whārite.
Koia nei te ara taurangi hei whakaoti i ēnei whārite tukutahi:
