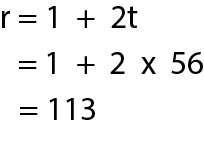WhakamĀrama Āpitihanga
Hei whakatauira i te rautaki āhuahanga. He raupapatanga tapatoru tēnei:

Mēnā ka whāia he rautaki āhuahanga hei whiriwhiri i te maha o ngā rārangi o te tapatoru-5, ka tuhia he pikitia, ka hangaia rānei te tauira kia 5 ngā tapatoru, ā, ka tatauria ngā rārangi (ka 11). He uaua, he nui hoki te mahi hei whiriwhiri i te maha o ngā rārangi o te tapatoru-56 mā te rautaki āhuahanga. He whaihua ake te rautaki taurangi. Hei tauira:
Ka āta tirohia te tipu o te raupapatanga tapatoru:

Tērā e kitea te tauira o te raupapatanga, arā, ka whakareatia te maha o ngā tapatoru ki te 2, me te tāpiri anō i te 1. Ko te whārite: r = 1 + 2t (r = te maha o ngā rārangi, t = te maha o ngā tapatoru). Nō reira, hei tātai i te maha o ngā rārangi o te tapatoru-56: